实现几个经典排序算法

冒泡排序

冒泡排序实现思路

冒泡排序算法相对其他排序运行效率较低，但是在概念上他是排序算法中最简单的

思路：

  1. 依次比较相邻的数字，如果前一个比后一个大，那么就交换。 即 小数放在前，大数放在后边。
  2. 然后比较第2个数和第3个数，小数在前，大数在后，依次类推则将最大的数滚动到最后边。
  3. 开始第二趟，将第二大的数移动至倒数第二位
  4. 依次类推…..

最后需要 第 （n-1） 趟就能完成排序。

参考动画：
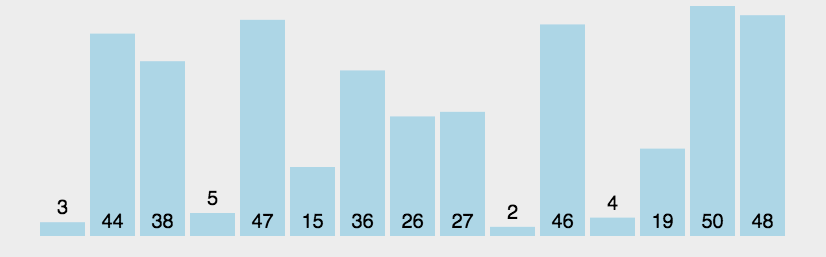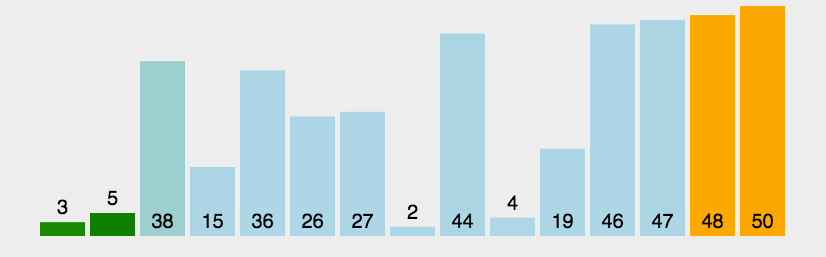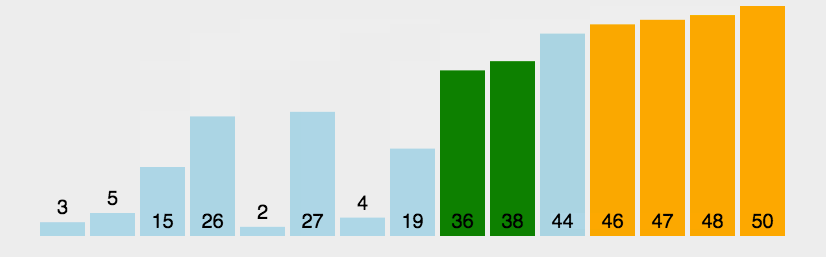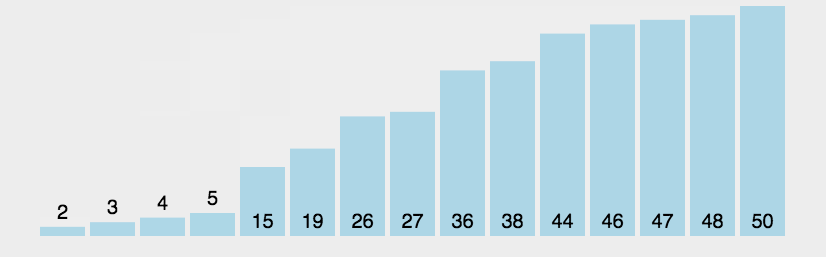
冒泡排序动画

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class ArrayList {
  array = []
  // 用于插入数据
  insert(item) {
    this.array.push(item)
  }
  swap(m,n) {
    let temp = this.array[m]
    this.array[m] = this.array[n]
    this.array[n] = temp
  }

 // 冒泡排序  （核心代码在这里）
  bubblesSort() {
    if (this.array === null || this.array.length < 2) { return }
    // 这里注意需要 length -1 。 原因是 如果是最后一个数会有bug，因为没有 第最后一个数+1的数
    // 也可以理解将 length -1 为 比较的次数
    for (let j = this.array.length - 1; j >= 0; j--) {
      for (let i = 0; i < j; i++) {
        if (this.array[i] > this.array[i + 1]) {
          this.swap(i, i + 1)
        }
      }
    }
  }


let list = new ArrayList()
list.insert(12)
list.insert(2)
list.insert(45)
list.insert(123)
list.insert(481)
list.insert(56)
console.log(list.array);   // [ 12, 2, 45, 123, 481, 56 ]


// 调用冒泡排序
list.bubblesSort()
console.log(list.array);  // [ 2, 12, 45, 56, 123, 481 ]

冒泡排序的效率

冒泡排序的比较次数（假设每一次比较都需要交换）：

  • 按照代码中来说，一共有6个数字
  • 第一次循环进行 6 次比较，第二次循环进行 5 次比较，第三次循环进行 4 次比较…..直到最后一趟进行一次比较
  • 对于 6 个数据来说就是： 6+5+4+3+2+1 次
  • 那么对于 n 个数据来就是： (n-1) + (n-2) + (n-3) + …..+ 1 = *n * (n-1) / 2*

通过大O表示法来推，则为 O(N²)

因为只考虑了每一次比较就需要交换， 所有大致的平均时间复杂度为: O(N²)

选择排序

选择排序实现思路

思路：

从第一个数开始与后面的每个数进行比较，找出最小的（默认是升序），然后交换，以此类推，直到排序结束。

代码实现步骤思路：

  1. 先取出第一个数的下标值为变量 min ， 循环遍历数组的长度
  2. 在循环中 用第一个数 分别比较每个数，最后将最小的数的下标值赋值给 min
  3. 将俩个数交换。这样就实现了第一个数为最小值
  4. 最后在整体套个循环，循环上面的思路即可

参考动画：

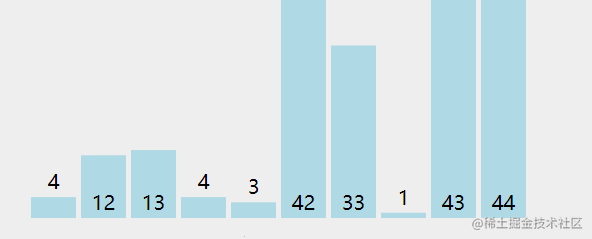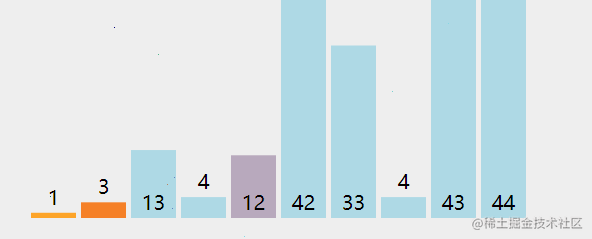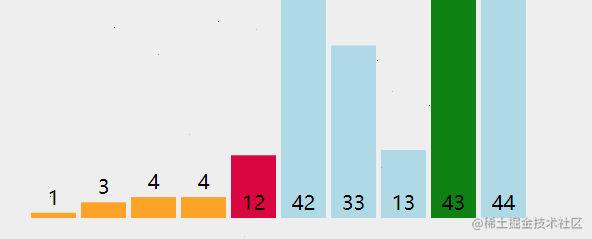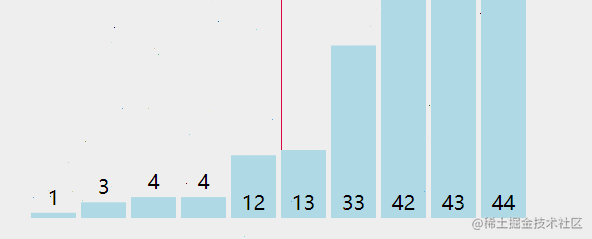
select.gif

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class ArrayList {
  array = [];

  // 用于插入数字
  insert(item) {
    this.array.push(item);
  }

  // 交换两个数字
  swap(m, n) {
    let temp = this.array[m];
    this.array[m] = this.array[n];
    this.array[n] = temp;
  }



  // 选择排序
  selectSort() {
    // 外部的循环表示 : 从0的位置开始取出数据，直到倒数第二个数的位置，即 length - 2
    for (let j = 0; j < this.array.length - 1; j++) {
      let min = j;
      // 内部的循环表示：从 min+1位置开始，和后面的数进行比较
      for (let i = min + 1; i < this.array.length; i++) {
        if (this.array[min] > this.array[i]) {
          min = i;
        }
      }
      this.swap(min, j);
    }
  }
  
}

let list = new ArrayList();
list.insert(12);
list.insert(2);
list.insert(45);
list.insert(123);
list.insert(481);
list.insert(56);
console.log(list.array); // [ 12, 2, 45, 123, 481, 56 ]


// 调用选择排序
list.selectSort();
console.log(list.array); // [ 2, 12, 45, 56, 123, 481 ]

选择算法效率

同样和冒泡排序效率差不多

时间复杂度:O(N²)

插入排序

插入排序思路

插入排序是简单排序中效率最好的一种

插入排序也是学习其他高级排序的基础，比如快速排序，

插入排序思想的核心 局部有序（部分有序）

思路:

  • 从 i 等于 1 开始变量，拿到当前数 current，与前面的数进行比较
  • 用while进行循环，如果前面的数大于当前的数，那么就进行交换。
  • 最好在外部套个循环，直到未排序的数没有了，那么排序就结束。

参考动画：

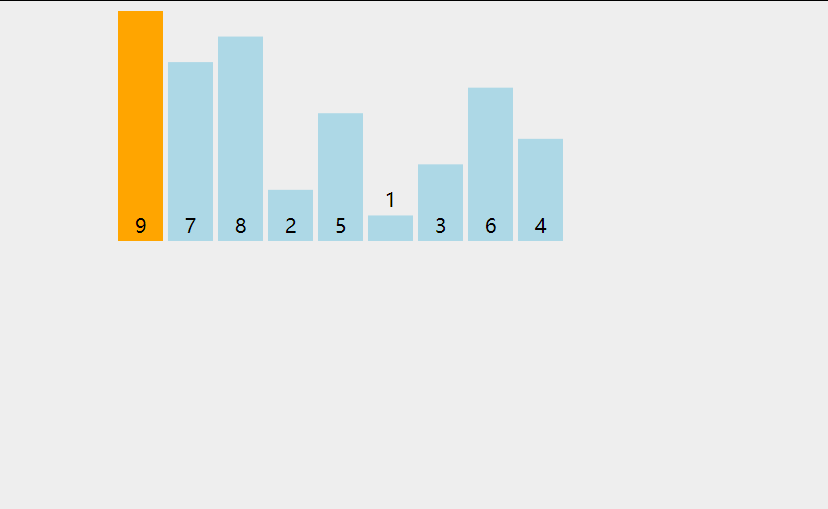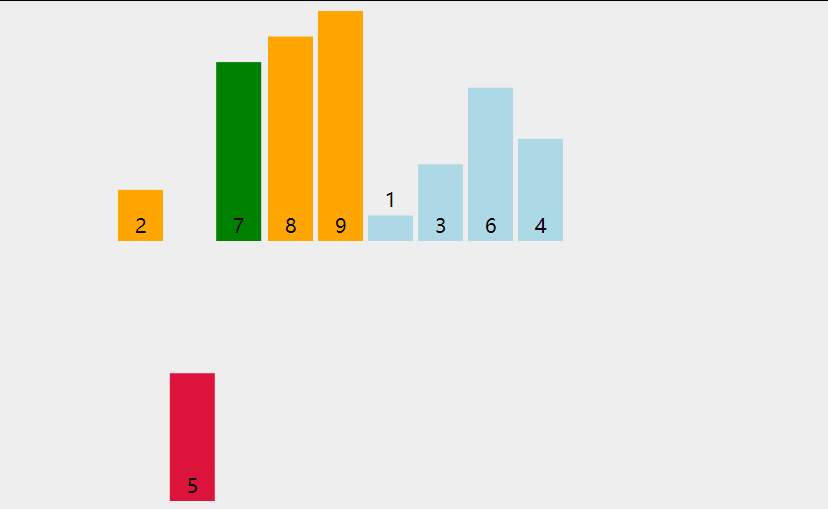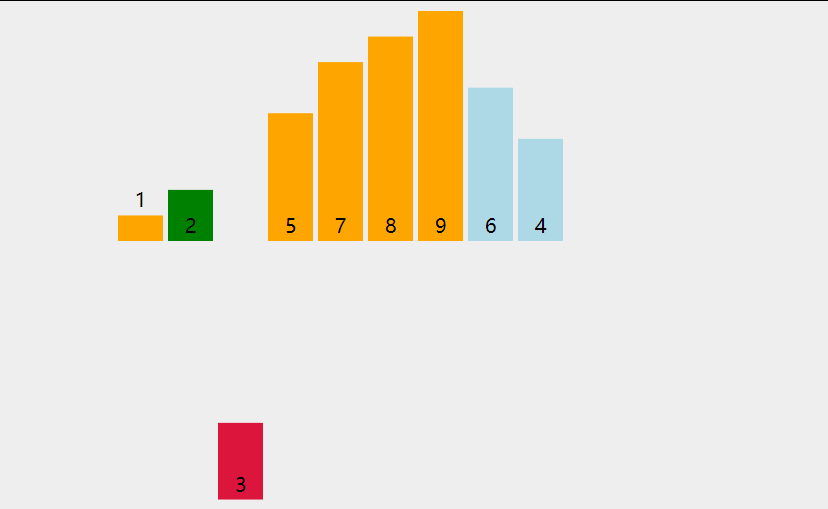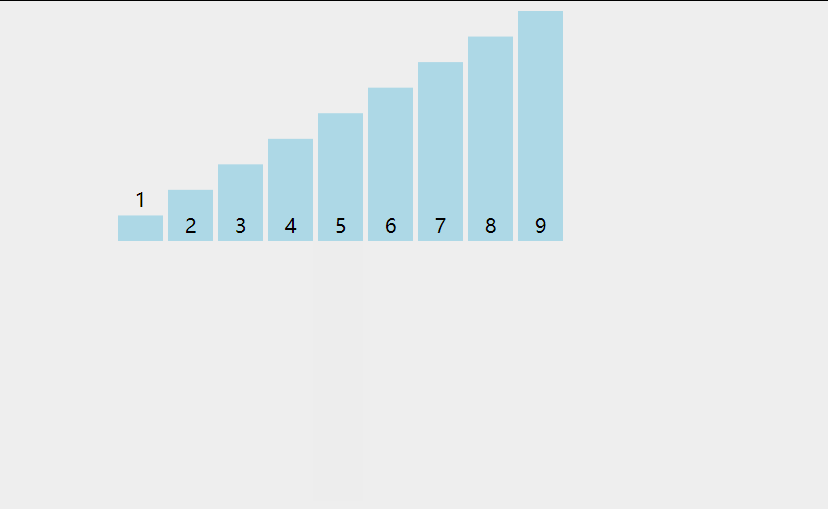
insert.gif

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class ArrayList {
  array = [];

  // 用于插入数字
  insert(item) {
    this.array.push(item);
  }


  //  插入排序
  insertSort() {
    for (let i = 1; i < this.array.length; i++) {
      let j = i; // 获取当前的下标值，存起来。
      let current = this.array[i];  // 获取当前的数，存起来
    // 由于不确定循环次数，所有用while
      while (this.array[j - 1] > current && j > 0) { 
      // 如果当前数的前一个比当前数大，就交换。
        this.array[j] = this.array[j - 1];
        j--;
      }
      // 将j位置的数，放到当前位置。
      this.array[j] = current;
    }
  }
}

let list = new ArrayList();
list.insert(12);
list.insert(2);
list.insert(45);
list.insert(123);
list.insert(481);
list.insert(56);
console.log(list.array);  // [ 12, 2, 45, 123, 481, 56 ]

// 调用 插入排序
list.insertSort();
console.log(list.array); // [ 2, 12, 45, 56, 123, 481 ]

插入排序的效率

插入排序的比较次数：

  • 第一趟时，需要的最多次数是1，第二趟最多次数是2，以此类推，最后一趟是 N-1 次
  • 因此插入排序比较的最多次数是：1+2+3+4+….+N-1 = N*(N-1) /2

插入排序的复制次数：

  • 第一趟时，需要的最多复制次数是1，第二趟最多次数是2，依次类推，最后一趟是N-1次
  • 因此复制最多次数是 ：1+2+3+4+….+N-1 = N*(N-1) /2
  • 平均次数是 N*(N-1) /4

所以时间复杂度为：O(N²)

快速排序

快速排序思路

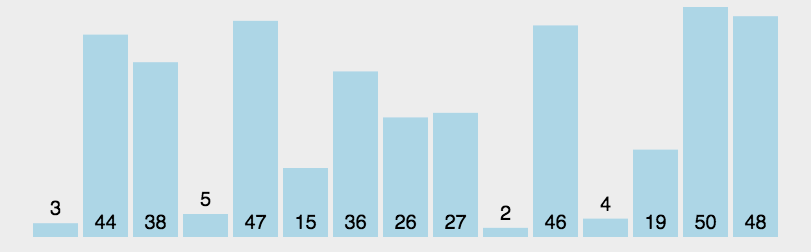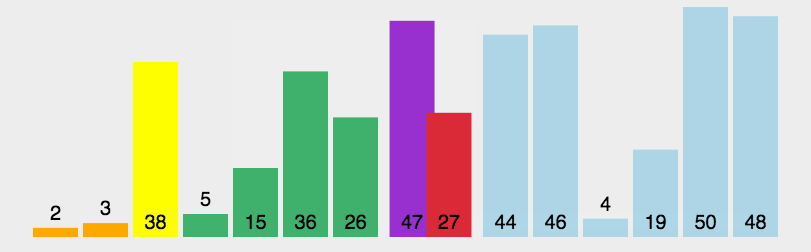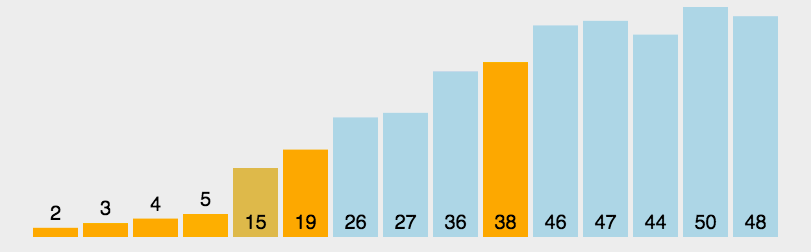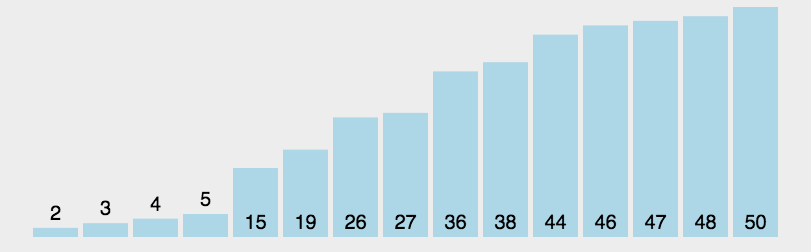
思路核心: 分而治之,即分成若个部分，逐个解决

思路:

  • 在数组中，选择一个数作为”基准”（pivot）。
  • 将数组分成左右俩部分，小于 基准 的放在左部分，大于 基准 的放在右部分。
  • 对”基准”左部分和右部分，不断重复第一步和第二步，直到所有部分只剩下一个元素为止。

动画参考:
quick.gif

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class ArrayList {
  array = [];

  // 用于插入数字
  insert(item) {
    this.array.push(item);
  }

  // 快速排序
  quickSort() {
    const quick = (array) => {
      if (array.length <= 1) {return array;}
      let pivotIndex = Math.floor(array.length / 2);
      let pivot = array.splice(pivotIndex, 1)[0];
      let left = [];
      let right = [];
      for (let i = 0; i < array.length; i++) {
        if (array[i] > pivot) {
          right.push(array[i]);
        } else {
          left.push(array[i]);
        }
      }
      return quick(left).concat([pivot], quick(right));
    };
    return this.array = quick(this.array);
  }

}

let list = new ArrayList();
list.insert(12);
list.insert(2);
list.insert(45);
list.insert(123);
list.insert(481);
list.insert(56);
console.log(list.array);

// 调用快速排序
list.quickSort();
console.log(list.array);

快速排序的效率

时间复杂度: O(nlogn)

归并排序

归并排序思路

归并排序也是采用 分而治之 的思想

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

思路:
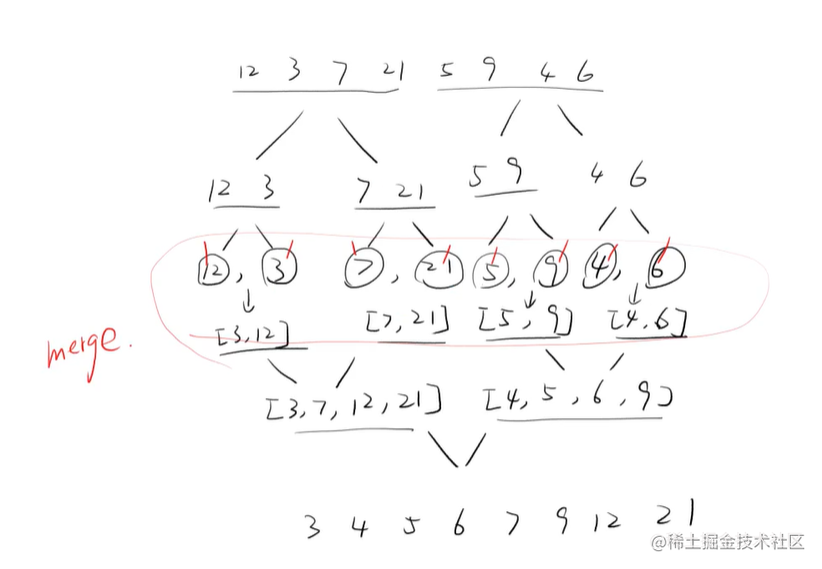
merge.png

动画参考:

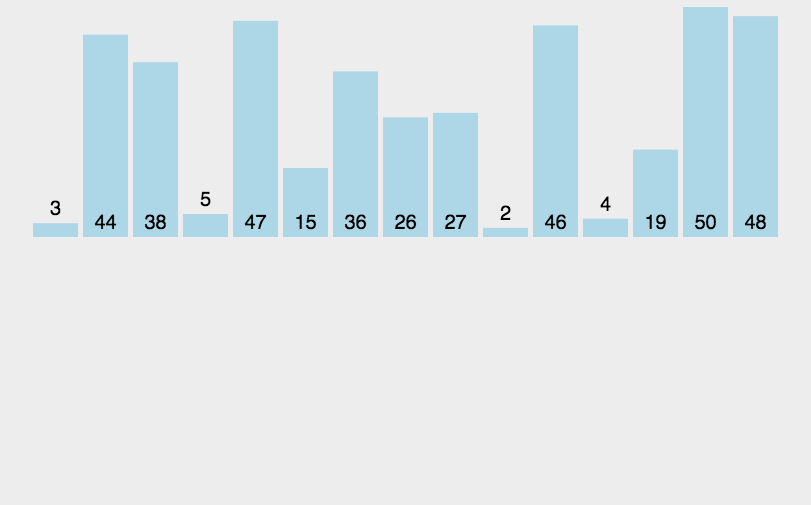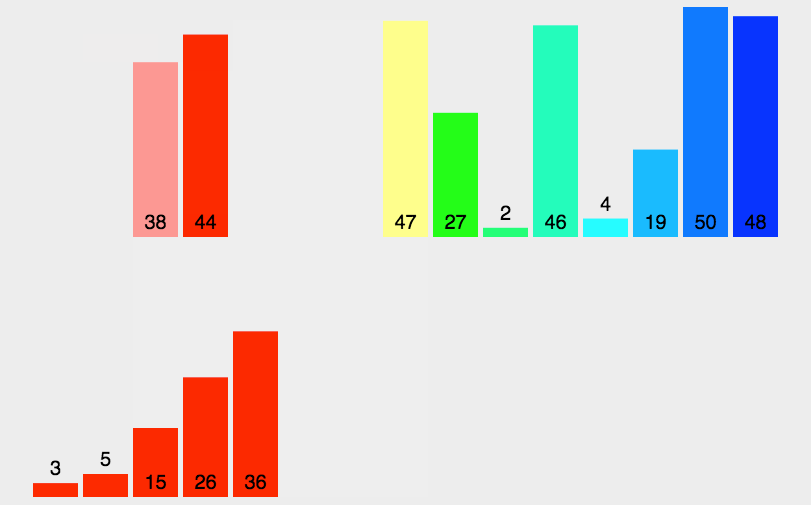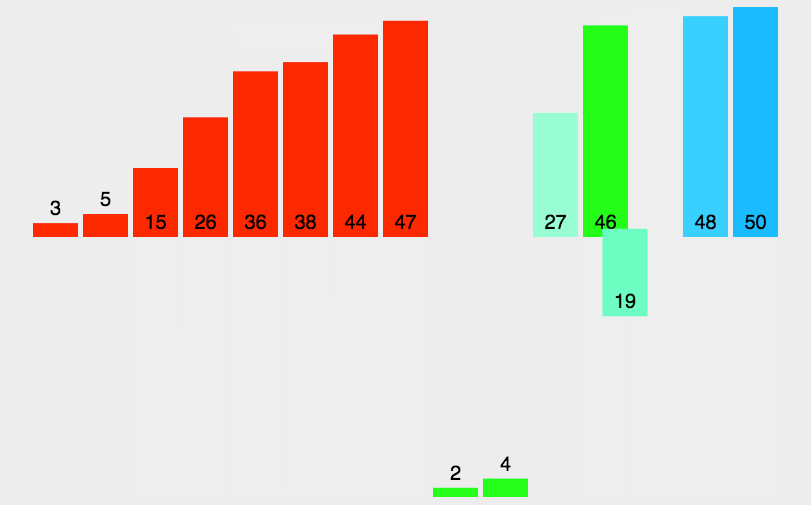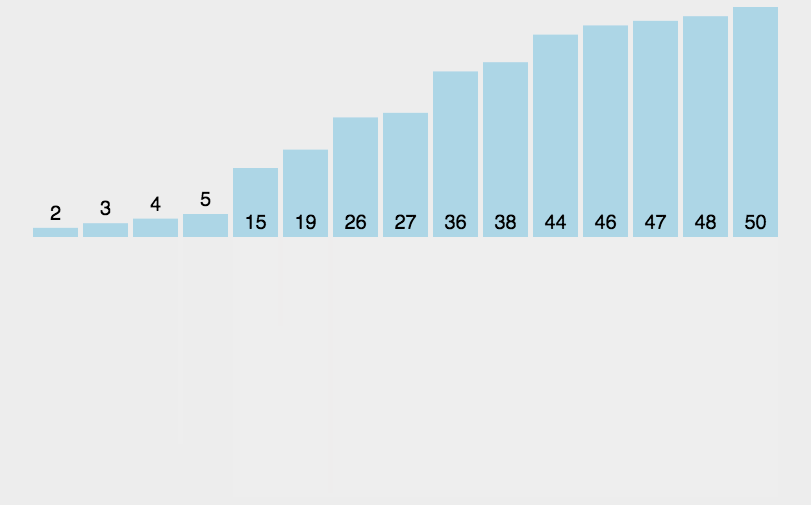
merge.gif

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class ArrayList {
  array = [];

  // 用于插入数字
  insert(item) {
    this.array.push(item);
  }

  // 归并排序
  mergeSort() {
    const mergerSorts = (array) => {
      if (array.length === 1) {return array;}
      let left = array.slice(0, Math.floor(array.length / 2));
      let right = array.slice(Math.floor(array.length / 2));
      const merge = (a, b) => {
        if (a.length === 0) return b;
        if (b.length === 0) return a;
        return a[0] < b[0] ? [a[0]].concat(merge(a.slice(1), b)) : [b[0]].concat(merge(a, b.slice(1)));
      };
      return merge(mergerSorts(left), mergerSorts(right));

    };
    return this.array = mergerSorts(this.array);
  }
}

let list = new ArrayList();
list.insert(12);
list.insert(2);
list.insert(45);
list.insert(123);
list.insert(481);
list.insert(56);
console.log(list.array);


// 调用归并排序
list.mergeSort();
console.log(list.array);

快速排序的效率

时间复杂度: O(nlogn)